Metric customization
The dissimilarity/similarity calculation for a pair of descriptor is represented by a metric. A default metric is associated for each descriptor which can be overriden when descriptor is calculated. In tool searchStorage the default metric can be overriden with command line option -metric <SPEC>. See detailed command line help printed with option -hm for applicable metric specifications. Various REST API endpoints support custom metric, usually with parameter metric. The format of the metric specification is the same for both the REST API and for searchStorage.
Using Web UI
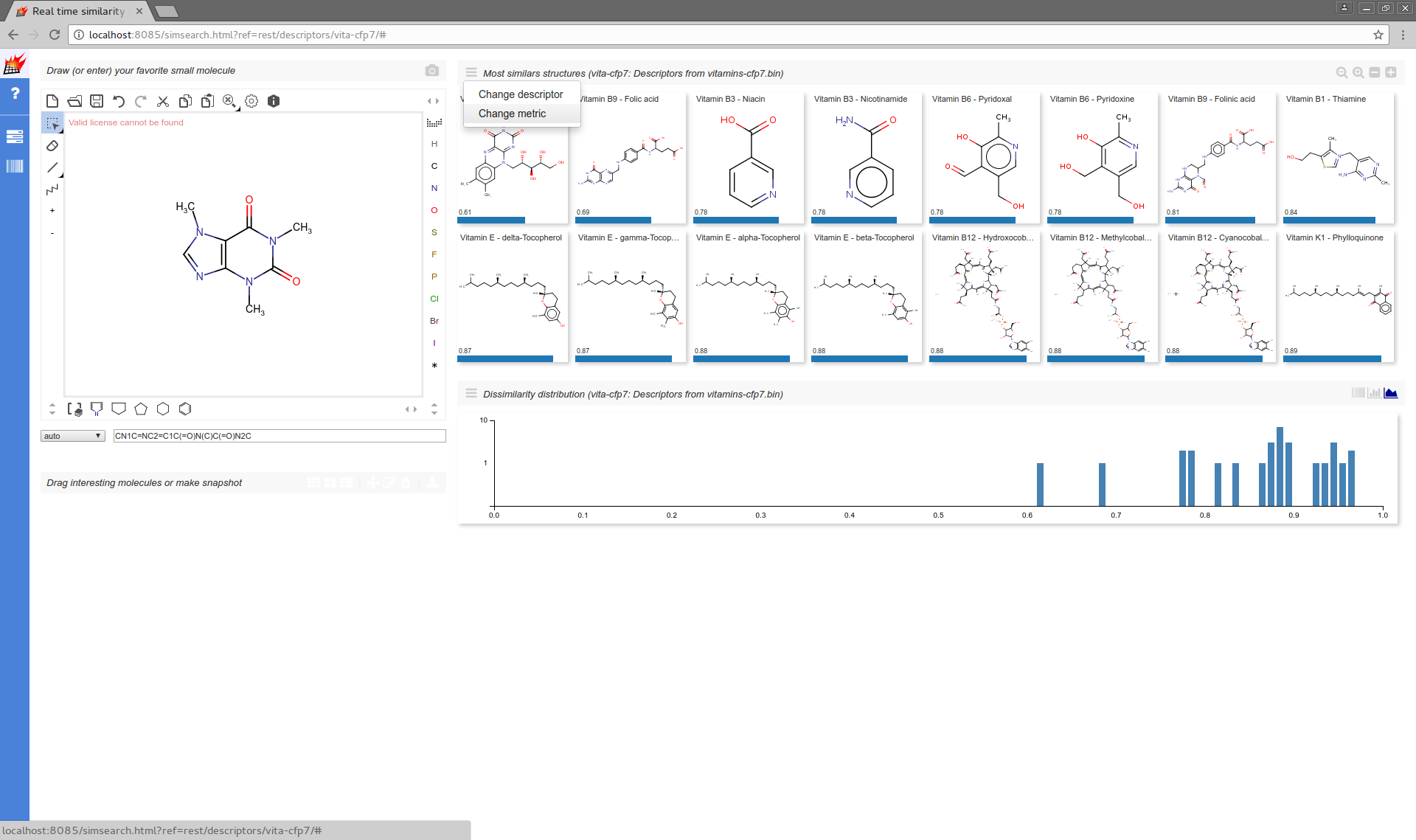
Web UI Most similar structures and Dissimilarity distribution support metric selection from their local menu:

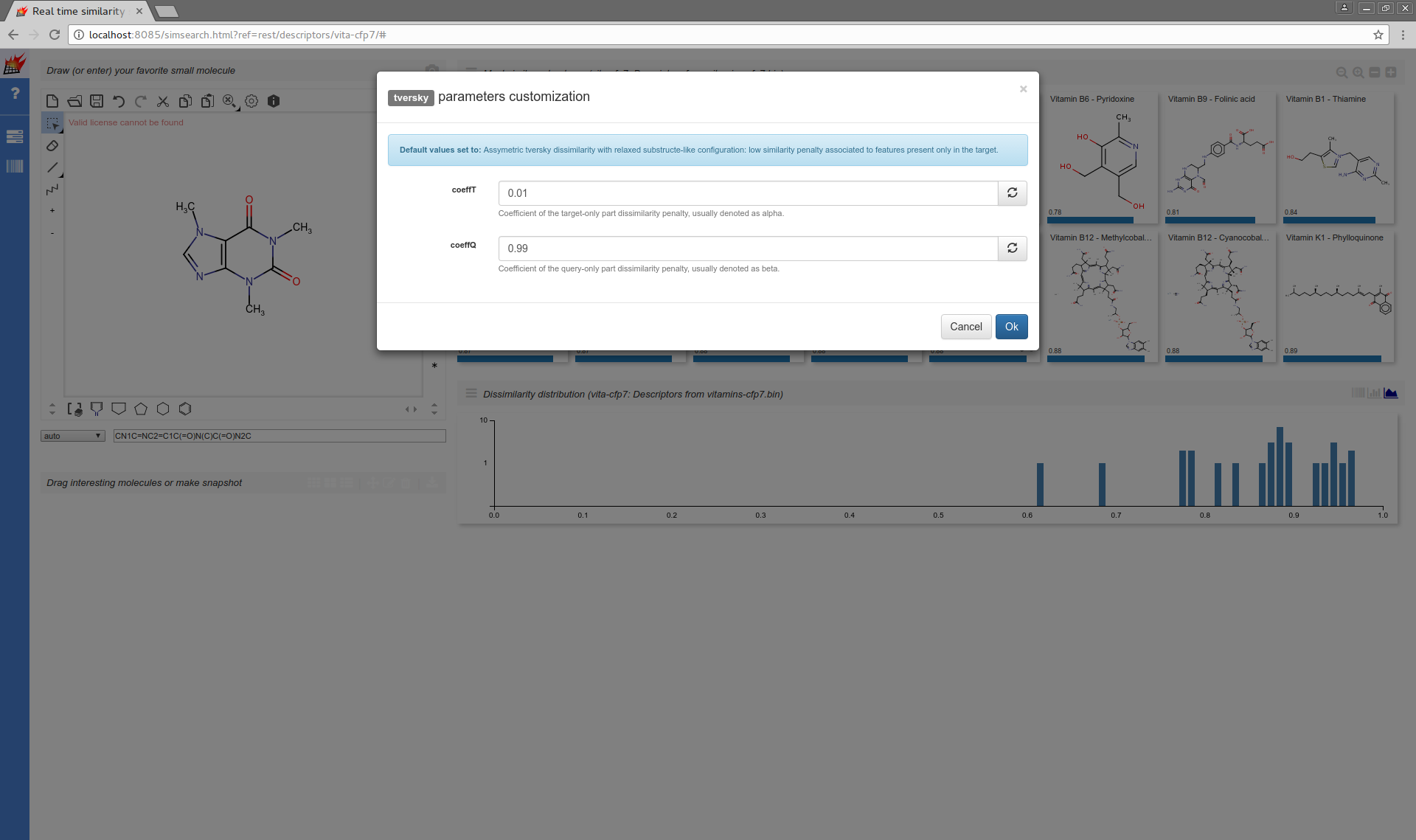
Modifying the default of parameterized metrics is also supported:
Format of metric specification
Argument passed to option -metric has the following generic format:
<COMMAND>[,<PARAMNAME_1>:<VALUE_1>] ... [,<PARAMNAME_n>:<VALUE_n>]
The actual commands and their parameterization depends on the descriptor type used.
Metrics for binary vector descriptors
The following table is taken from the output of searchStorage -hm.
| Metric specification | Description |
|---|---|
manhattan |
Dissimilarity value is calculated as the number of bit positions containing differing values. This measure is also known as "Taxicab geometry" |
manhattan_norm |
Dissimilarity value is calculated as the number of bit positions containing differing values. This measure is also known as "Taxicab geometry". Similarity/dissimilarity value range is normalized to the unit interval (0.0 - 1.0 including bounds). |
euclidean |
Dissimilarity value is calculated as the square root of the number of bit positions containing differing values. |
euclidean_norm |
Dissimilarity value is calculated as the square root of the number of bit positions containing differing values. Similarity/dissimilarity value range is normalized to the unit interval (0.0 - 1.0 including bounds). |
commonpart |
Similarity value is calculated as the bit positions containing set values in both compared descriptor. Dissimilarity value is calculated by substracting this common bit counts from the fingerprint length. |
commonpart_norm |
Similarity value is calculated as the bit positions containing set values in both compared descriptor. Dissimilarity value is calculated by substracting this common bit counts from the fingerprint length. Similarity/dissimilarity value range is normalized to the unit interval (0.0 - 1.0 including bounds) by dividing the values with the fingerprint length. |
dice |
Similarity coefficient is twice the size of common part divided by the sum of components. When comparing all-zero binary fingerprint we return minimal similarity (maximal dissimilarity). |
tanimoto |
Tanimoto similarity coefficient (often referred as Jaccard index) is calculated by dividing the size of intersection (number of bit positions set in both descriptor) with the size of the union (number of bit positions set in either descriptor). When comparing all-zero binary fingerprint we return minimal similarity (maximal dissimilarity). |
petke |
Petke or Braun-Blanquet similarity is calculated by dividing the size of the intersection with the maximum of the sizes of the two compared descriptors. When comparing all-zero binary fingerprints we return minimal similarity (maximal dissimilarity). |
simpson |
Simpson similarity (also known as overlap similarity) is calculated by dividing the size of the intersection with the minimum of the sizes of the two compared descriptors. When comparing all-zero binary fingerprints we return minimal similarity (maximal dissimilarity). |
tversky,coeffT:0.0,coeffQ:1.0 |
Assymetric tversky dissimilarity with substructure-like configuration: no similarity penalty associated to features present only in the target. |
tversky,coeffT:0.01,coeffQ:0.99 |
Assymetric tversky dissimilarity with relaxed substructe-like configuration: low similarity penalty associated to features present only in the target. |
tversky,coeffT:0.15,coeffQ:0.85 |
Assymetric tversky dissimilarity with more relaxed substructure-like configuration. |
tversky,coeffT:1.0,coeffQ:0.0 |
Assymetric tversky dissimilarity with superstructure-like configuration: no similarity penalty associated to features present only in the query. |
tversky,coeffT:0.99,coeffQ:0.01 |
Assymetric tversky dissimilarity with relaxed superstructure-like configuration: low similarity penalty associated to features present only in the query. |
tversky,coeffT:0.85,coeffQ:0.15 |
Assymetric tversky dissimilarity with more relaxed superstructure-like configuration. |
Metrics for float vector descriptors
The following table is taken from the output of searchStorage -hm.
| Metric configuration | Configuration description |
|---|---|
euclidean |
Dissimilarity value is calculated as the square root of the sums of the difference squares. |
euclidean_sqr |
Dissimilarity value is calculated as the sums of the difference squares. |
manhattan |
Sum of the absolute values of the differences. |
maximum |
Max of the absolute values of the differences. |
tanimoto_histogram |
Tanimoto similarity coefficient (often referred as Jaccard index) is calculated by dividing the size of intersection (maximal common value in bins/coordinates) with the size of the union (max value in bins). |
tversky,coeffT:0.0,coeffQ:1.0 |
Assymetric tversky dissimilarity with substructure-like configuration: no similarity penalty associated to features present only in the target. |
tversky,coeffT:0.01,coeffQ:0.99 |
Assymetric tversky dissimilarity with relaxed substructe-like configuration: low similarity penalty associated to features present only in the target. |
tversky,coeffT:0.15,coeffQ:0.85 |
Assymetric tversky dissimilarity with more relaxed substructure-like configuration. |
tversky,coeffT:1.0,coeffQ:0.0 |
Assymetric tversky dissimilarity with superstructure-like configuration: no similarity penalty associated to features present only in the query. |
tversky,coeffT:0.99,coeffQ:0.01 |
Assymetric tversky dissimilarity with relaxed superstructure-like configuration: low similarity penalty associated to features present only in the query. |
tversky,coeffT:0.85,coeffQ:0.15 |
Assymetric tversky dissimilarity with more relaxed superstructure-like configuration. |
Example using searchStorage
In the following example we calculate dissimilarities of custom binary vector fingerprints. Length of the fingerprint is 64 bit. See document Using cunstom mbinary descriptors for details.
Note that the fingerprint length is 64 bit, its value is represented by packed long values.
echo -e "...0000 0\n...0001 1\n...0011 3\n...0110 6\n...1111 15" | bin/importStorage.sh \
-in - \
-splitter com.chemaxon.overlap.splits.AllButFirstToken \
-idsplitter com.chemaxon.overlap.splits.FirstToken \
-out custom-fp.bin \
-id custom-fp-id.bin \
-contextjs "ctx_from_descpb(bld_bv.length(64).endianness(en_BIG_ENDIAN).stringFormat(sf_PACKED_LONG_TABSEP))"
bin/searchStorage.sh -frombytes custom-fp.bin -idstorage custom-fp-id.bin -mode FULLMATRIX -qd "6" -metric tanimoto
bin/searchStorage.sh -frombytes custom-fp.bin -idstorage custom-fp-id.bin -mode FULLMATRIX -qd "6" -metric manhattan
bin/searchStorage.sh -frombytes custom-fp.bin -idstorage custom-fp-id.bin -mode FULLMATRIX -qd "6" -metric manhattan_norm
bin/searchStorage.sh -frombytes custom-fp.bin -idstorage custom-fp-id.bin -mode FULLMATRIX -qd "6" -metric euclidean
bin/searchStorage.sh -frombytes custom-fp.bin -idstorage custom-fp-id.bin -mode FULLMATRIX -qd "6" -metric commonpart
bin/searchStorage.sh -frombytes custom-fp.bin -idstorage custom-fp-id.bin -mode FULLMATRIX -qd "6" -metric commonpart_norm
bin/searchStorage.sh -frombytes custom-fp.bin -idstorage custom-fp-id.bin -mode FULLMATRIX -qd "6" -metric tversky,coeffT:0.0,coeffQ:1.0
bin/searchStorage.sh -frombytes custom-fp.bin -idstorage custom-fp-id.bin -mode FULLMATRIX -qd "6" -metric tversky,coeffT:0.01,coeffQ:0.99
bin/searchStorage.sh -frombytes custom-fp.bin -idstorage custom-fp-id.bin -mode FULLMATRIX -qd "6" -metric tversky,coeffT:0.15,coeffQ:0.85
Dissimilarity values returned from searches above:
| Target | tanimoto |
manhattan |
manhattan_norm |
euclidean |
commonpart |
commonpart_norm |
tversky,coeffT:0.0,coeffQ:1.0 |
tversky,coeffT:0.01,coeffQ:0.99 |
|---|---|---|---|---|---|---|---|---|
...0000 |
1.0 | 2.0 | 0.03125 | 1.4142... | 64.0 | 1.0 | 1.0 | 1.0 |
...0001 |
1.0 | 3.0 | 0.046875 | 1.7320... | 64.0 | 1.0 | 1.0 | 1.0 |
...0011 |
0.66666 | 2.0 | 0.03125 | 1.4142... | 63.0 | 0.984375 | 0.5 | 0.5 |
...0110 |
0.0 | 0.0 | 0.0 | 0.0 | 62.0 | 0.96875 | 0.0 | 0.0 |
...1111 |
0.5 | 2.0 | 0.03125 | 1.4142... | 62.0 | 0.96875 | 0.0 | 0.0099... |
Notes for this example:
- The fingerprints are 64 bits long, represented by one 64 bit
longvalue: the binary value of the decimal number (6from line...0110 6) is used as the bit vector. - The leading binary strings (
...0110from line...0110 6) are used as textual IDs for display purpose. - The query descriptor is the same as the 4th descriptor used (having id
...0110and packed long representation6). The query descriptor in its binary form is0000000000000000000000000000000000000000000000000000000000000110. - Normalized (
..._norm) metrics scale the dissimilarity range to0.0..1.0interval - Metrics
commonpartandcommonpart_normassociate non-zero dissimilarity value for identical fingerprints.
Example using the REST API - Similarity search
Expose the custom descriptors from the previous example over the REST API:
echo -e "...0000 0\n...0001 1\n...0011 3\n...0110 6\n...1111 15" | bin/importStorage.sh \
-in - \
-splitter com.chemaxon.overlap.splits.AllButFirstToken \
-idsplitter com.chemaxon.overlap.splits.FirstToken \
-out custom-fp.bin \
-id custom-fp-id.bin \
-contextjs "ctx_from_descpb(bld_bv.length(64).endianness(en_BIG_ENDIAN).stringFormat(sf_PACKED_LONG_TABSEP))"
bin/gui.sh \
-idonly -name:custom-fp-id:-mid:custom-fp-id.bin \
-desc -desc:custom-fp.bin:-mols:custom-fp-id:-name:custom-fp \
-nobrowse \
-port 8085
Query the server using curl with POST requests. Note that the targets are sorted by dissimilarity.
curl \
-X POST \
-d "query-descriptor=6" \
-d "max-count=10" \
-g \
"http://localhost:8085/rest/descriptors/custom-fp/find-most-similars-by-descriptor" | python -m json.tool
{
"query": "6",
"querysmi": null,
"searchtime": 0,
"targetcount": 5,
"targets": [
{
"base64img": null,
"dissimilarity": 0.0,
"targetid": "...0110",
"targetimageurl": "rest/molecules/custom-fp-id/3/png-or-placeholder?w=100&h=100",
"targetindex": 3,
"targetmolurl": "rest/molecules/custom-fp-id/3"
},
{
"base64img": null,
"dissimilarity": 0.5,
"targetid": "...1111",
"targetimageurl": "rest/molecules/custom-fp-id/4/png-or-placeholder?w=100&h=100",
"targetindex": 4,
"targetmolurl": "rest/molecules/custom-fp-id/4"
},
{
"base64img": null,
"dissimilarity": 0.6666666666666666,
"targetid": "...0011",
"targetimageurl": "rest/molecules/custom-fp-id/2/png-or-placeholder?w=100&h=100",
"targetindex": 2,
"targetmolurl": "rest/molecules/custom-fp-id/2"
},
{
"base64img": null,
"dissimilarity": 1.0,
"targetid": "...0000",
"targetimageurl": "rest/molecules/custom-fp-id/0/png-or-placeholder?w=100&h=100",
"targetindex": 0,
"targetmolurl": "rest/molecules/custom-fp-id/0"
},
{
"base64img": null,
"dissimilarity": 1.0,
"targetid": "...0001",
"targetimageurl": "rest/molecules/custom-fp-id/1/png-or-placeholder?w=100&h=100",
"targetindex": 1,
"targetmolurl": "rest/molecules/custom-fp-id/1"
}
]
}
curl \
-X POST \
-d "query-descriptor=6" \
-d "max-count=10" \
-d "metric=manhattan" \
-g \
"http://localhost:8085/rest/descriptors/custom-fp/find-most-similars-by-descriptor" | python -m json.tool
{
"query": "6",
"querysmi": null,
"searchtime": 0,
"targetcount": 5,
"targets": [
{
"base64img": null,
"dissimilarity": 0.0,
"targetid": "...0110",
"targetimageurl": "rest/molecules/custom-fp-id/3/png-or-placeholder?w=100&h=100",
"targetindex": 3,
"targetmolurl": "rest/molecules/custom-fp-id/3"
},
{
"base64img": null,
"dissimilarity": 2.0,
"targetid": "...0000",
"targetimageurl": "rest/molecules/custom-fp-id/0/png-or-placeholder?w=100&h=100",
"targetindex": 0,
"targetmolurl": "rest/molecules/custom-fp-id/0"
},
{
"base64img": null,
"dissimilarity": 2.0,
"targetid": "...0011",
"targetimageurl": "rest/molecules/custom-fp-id/2/png-or-placeholder?w=100&h=100",
"targetindex": 2,
"targetmolurl": "rest/molecules/custom-fp-id/2"
},
{
"base64img": null,
"dissimilarity": 2.0,
"targetid": "...1111",
"targetimageurl": "rest/molecules/custom-fp-id/4/png-or-placeholder?w=100&h=100",
"targetindex": 4,
"targetmolurl": "rest/molecules/custom-fp-id/4"
},
{
"base64img": null,
"dissimilarity": 3.0,
"targetid": "...0001",
"targetimageurl": "rest/molecules/custom-fp-id/1/png-or-placeholder?w=100&h=100",
"targetindex": 1,
"targetmolurl": "rest/molecules/custom-fp-id/1"
}
]
}
curl \
-X POST \
-d "query-descriptor=6" \
-d "max-count=10" \
-d "metric=tversky,coeffT:0.0,coeffQ:1.0" \
-g \
"http://localhost:8085/rest/descriptors/custom-fp/find-most-similars-by-descriptor" | python -m json.tool
{
"query": "6",
"querysmi": null,
"searchtime": 3,
"targetcount": 5,
"targets": [
{
"base64img": null,
"dissimilarity": 0.0,
"targetid": "...0110",
"targetimageurl": "rest/molecules/custom-fp-id/3/png-or-placeholder?w=100&h=100",
"targetindex": 3,
"targetmolurl": "rest/molecules/custom-fp-id/3"
},
{
"base64img": null,
"dissimilarity": 0.0,
"targetid": "...1111",
"targetimageurl": "rest/molecules/custom-fp-id/4/png-or-placeholder?w=100&h=100",
"targetindex": 4,
"targetmolurl": "rest/molecules/custom-fp-id/4"
},
{
"base64img": null,
"dissimilarity": 0.5,
"targetid": "...0011",
"targetimageurl": "rest/molecules/custom-fp-id/2/png-or-placeholder?w=100&h=100",
"targetindex": 2,
"targetmolurl": "rest/molecules/custom-fp-id/2"
},
{
"base64img": null,
"dissimilarity": 1.0,
"targetid": "...0000",
"targetimageurl": "rest/molecules/custom-fp-id/0/png-or-placeholder?w=100&h=100",
"targetindex": 0,
"targetmolurl": "rest/molecules/custom-fp-id/0"
},
{
"base64img": null,
"dissimilarity": 1.0,
"targetid": "...0001",
"targetimageurl": "rest/molecules/custom-fp-id/1/png-or-placeholder?w=100&h=100",
"targetindex": 1,
"targetmolurl": "rest/molecules/custom-fp-id/1"
}
]
}
Example using REST API - Dissimilarity distribution
Expose the custom descriptors from the previous example over the REST API:
echo -e "...0000 0\n...0001 1\n...0011 3\n...0110 6\n...1111 15" | bin/importStorage.sh \
-in - \
-splitter com.chemaxon.overlap.splits.AllButFirstToken \
-idsplitter com.chemaxon.overlap.splits.FirstToken \
-out custom-fp.bin \
-id custom-fp-id.bin \
-contextjs "ctx_from_descpb(bld_bv.length(64).endianness(en_BIG_ENDIAN).stringFormat(sf_PACKED_LONG_TABSEP))"
bin/gui.sh \
-idonly -name:custom-fp-id:-mid:custom-fp-id.bin \
-desc -desc:custom-fp.bin:-mols:custom-fp-id:-name:custom-fp \
-nobrowse \
-port 8085
Query the server using curl with POST requests.
curl \
-X POST \
-d "query-descriptor=6" \
-d "bins=4" \
-d "l=-0.5" \
-d "h=3.5" \
-d "metric=manhattan" \
-g \
"http://localhost:8085/rest/descriptors/custom-fp/distribution-by-descriptor" | python -m json.tool
The dissimilarity values 2.0, 3.0, 2.0, 0.0 and 2.0 which are shown in the result histogram:
{
"histogram": {
"bincount": 4,
"bins": [
1,
0,
3,
1
],
"binwidth": 1.0,
"h": 3.5,
"highcount": 0,
"l": -0.5,
"lowcount": 0,
"maxBinValue": 3,
"totalcount": 5
},
"searchtime": 0,
"targetcount": 5
}